7.11. Двоичные деревья.

Не считая линейных структур существуют и нелинейные, при помощи которых задаются иерархические связи данных. Для этого употребляются графы, а среди них сетевые и древовидные структуры. Разглядим один вид деревьев — двоичное дерево.

Двоичное (бинарное) дерево — это конечное множество элементов, которое или пусто, или содержит один элемент, именуемый корнем дерева, а остальные элементы множества делятся на два непересекающихся подмножества, каждое из которых само есть двоичным деревом. Эти подмножества именуются левым и правым поддеревьями исходного дерева.

Рис. 8 Бинарное дерево

На рис. 8 продемонстрирован чаще всего видящийся метод представления двоичного дерева. Оно складывается из девяти узлов.

Корнем дерева есть узел А. Левое поддерево имеет корень В, а правое поддерево — корень С. Они соединяются соответствующими ветвями, исходящими из А. Отсутствие ветви свидетельствует безлюдное поддерево. К примеру, у поддерева с корнем С нет левого поддерева, оно пусто. Пусто и правое поддерево с корнем Е. Двоичные поддеревья с корнями D. G. H и I имеют правые и пустые левые поддеревья.

Узел, имеющий безлюдные правое и левое поддеревья, именуется страницей. В случае если любой узел двоичного дерева, не являющийся страницей, имеет непустые правое и левое поддеревья, то дерево именуется строго двоичным

Уровень узла в двоичном дереве определяется следующим образом: уровень корня неизменно равен нулю, а потом номера уровней при перемещении по дереву от корня возрастают на 1 по отношению к собственному яркому предку. Глубина двоичного дерева — это большой уровень страницы дерева, в противном случае говоря, протяженность самого долгого пути от корня к странице дерева. Узлы дерева смогут быть пронумерованы по следующей схеме (см. рис. 9)

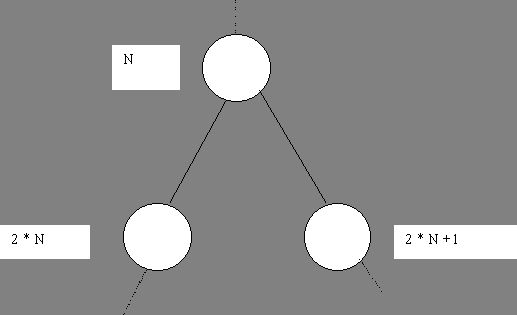
Рис. 9 Схема нумерации узлов бинарного дерева

Номер корня неизменно равен 1, левый потомок приобретает номер 2, правый — номер 3. Левый потомок узла 2 обязан взять номер 4, а правый — 5, левый потомок узла 3 возьмёт номер 6, правый — 7 и т.д. Несуществующие узлы не нумеруются, что, но, не нарушает указанного порядка, поскольку их номера не употребляются. При таковой совокупности нумерации в дереве любой узел приобретает неповторимый номер.

Полное двоичное дерево уровня n — это дерево, в котором любой узел уровня n есть страницей и любой узел уровня меньше n имеет непустые правое и левое поддеревья.

Практически полное двоичное дерево определяется как двоичное дерево, для которого существует неотрицательное целое k такое, что:

1) любой лист в дереве имеет уровень k либо k +1;

2) в случае если узел дерева имеет правого потомка уровня k +1, тогда все его левые потомки, являющиеся страницами, кроме этого имеют уровень k +1.

7 .12. Действия с двоичными деревьями.

Разглядывая действия над деревьями, возможно заявить, что для построения дерева нужно вырабатывать узлы, и, выяснив предварительно место включения, включать их в дерево. Количество узлов определяется необходимостью. Метод включения должен быть известен и постоянен. Узлы

дерева смогут быть использованы для хранения какой-либо информации.

Потом нужно осуществлять поиск заданного узла в дереве. Это возможно организовать, к примеру, последовательно обходя узлы дерева, причем любой узел должен быть просмотрен лишь один раз.

Может появиться уничтожения и задача дерева в тот момент, в то время, когда необходимость в нем (в информации, записанной в его элементах) отпадает. Во многих случаях может потребоваться уничтожение поддерева.

Чтобы совокупность узлов образовала дерево, нужно каким-то образом вырабатывать и применять связи узлов со потомками и своими предками. Все это сильно напоминает действия над элементами перечня.

Ответственным понятием древовидной структуры есть понятие бинарного дерева поиска. Правило построения бинарного дерева поиска: элементы, у которых значение некоего показателя меньше, чем у корня, постоянно включаются слева от некоего поддерева, а элементы со значениями, громадными, чем у корня — справа. Данный принцип употребляется и при формировании бинарного дерева, и при поиске в нем элементов.

Так, при поиске элемента с некоторым значением показателя происходит спуск по дереву, начиная от корня, причем выбор ветви следующего шага — направо либо налево в соответствии с значению искомого показателя — происходит в каждом очередном узле на этом пути. При поиске элемента результатом будет или отысканный узел с заданным значением показателя, или поиск закончится страницей с «нулевой» ссылкой, а требуемый элемент отсутствует на проделанном по дереву пути. В случае если поиск был проделан для включения очередного узла в дерево, то в следствии будет отыскан узел с безлюдной ссылкой (безлюдными ссылками), к которому справа либо слева в соответствии со значением показателя и будет присоединен новый узел.

Разглядим пример формирования бинарного дерева. Предположим, что необходимо организовать бинарное дерево, узлы (элементы) которого имеют следующие значения показателя: 20, 10, 35, 15, 17, 27, 24, 8, 30. В этом же порядке они и будут поступать для включения в бинарное дерево. Первым узлом в дереве (корнем) станет узел со значением 20.

Обратить внимание: поиск места подключения очередного элемента постоянно начинается с корня. К корню слева подключается элемент 10. К корню справа подключается элемент 35.

Потом элемент 15 подключается справа к 10, проходя путь: корень 20 — налево — элемент 10 — направо — подключение, поскольку дальше пути нет. Процесс длится до исчерпания включаемых элементов. Итог представлен на рис.

10.

Рис. 10 Построение двоичного дерева.

Значения элементов дерева: 20, 10, 35, 15, 17, 27, 24, 8, 30

При создании бинарного дерева раздельно решается вопрос с возможностью включения элементов с дублирующими показателями. Метод бинарного поиска разрешает при включении корректно расположить узлы в дереве, но при поиске уже включенных элементов появляются сложности, поскольку при стандартном варианте поиска будет выбираться лишь один из дублей. Для обнаружения всех дублей должен быть применен метод для того чтобы обхода дерева, при котором любой узел дерева будет выбран один раз.

7 .13. Ответ задач работы с двоичным деревом.

Источник: www.declic.narod.ru

08 — Введение в алгоритмы. Деревья и двоичные деревья

Важное на сайте:

• Что такое биржа. какую биржу выбрать для торгов
• Что такое биржа трейдеров
• Что такое cfd на форекс
• Что такое экспирация фьючерсов?
• Что такое элективный курс

Самые интересные результаты статей, подобранные именно по Вашим интересам:

• Как читать графики бинарных опционов?

  Торговля двоичными опционами сулит хорошую прибыль, но для успеха в этом виде дохода нужно владеть навыками фундаментального и теханализа. Умение…

• Бинарные часы на atmega32

  Опубликовано 22 Июль 2015. Размещено в Устройства на AVR Рейтинг: / 1 Не хорошо Превосходно Началось все с того что захотелось сделать какое-нибудь…

• Как решать бинарные уравнения

  20010,0,3500, 63. Двучленные уравнения. Алгебраическое уравнение вида называется двучленным уравнением. Решение такого уравнения просто сводится к…

• Бинарные часы как ими пользоваться

  Двоичные часы Я намерено написал эту статью для тех, кто не знает, как пользоваться двоичными часами. А все вследствие того что я приобрел эти часы и…

• Как выбрать надежного брокера бинарных опционов

  В данной статье мы желаем дать читателю пара советов про то, как выяснить надежного брокера двоичных опционов на рынке. Эта тема достаточно актуальна и…

• Как заработать на бинарных опционах новичку

  Как и каждый вид деятельности, торговля двоичными опционами требует определенной подготовки. Само собой разумеется, реклама говорит нам, что торговать…