Часть 3. Способы прикладной статистики

3.2.1. Коэффициенты корреляции

Термин корреляция свидетельствует сообщение. В эконометрике данный термин в большинстве случаев употребляется в сочетании коэффициенты корреляции. Разглядим линейный и непараметрические парные коэффициенты корреляции.

Обсудим методы измерения связи между двумя случайными переменными. Пускай исходными данными есть комплект случайных векторов  Выборочным коэффициентом корреляции, более детально, выборочным линейным парным коэффициентом корреляции К. Пирсона, как мы знаем, именуется число

В случае если rn = 1, то

 причем a 0. В случае если же rn = — 1, то

 причем a 0. Так, близость коэффициента корреляции к 1 (по полной величине) говорит о достаточно тесной линейной связи.

В случае если случайные вектора

 свободны и одинаково распределены, то выборочный коэффициент корреляции сходится к теоретическому при бесконечном возрастании количества выборки:

(сходимость по возможности).

Более того, выборочный коэффициент корреляции есть асимптотически обычным. Это указывает, что

где

— функция стандартного обычного распределения с дисперсией и 0 математическим ожиданием 1, а

— асимптотическая дисперсия выборочного коэффициента корреляции. Она имеет сверхсложное выражение, приведенное в монографии [1, с.393]:

Тут под

 понимаются теоретические центральные моменты порядка k и m. в частности,

.

Коэффициенты корреляции типа rn употребляются во многих методах многомерного статистического анализа. В теоретических рассмотрениях довольно часто уверены в том, что случайные вектора

 имеют двумерное

обычное распределение. Распределения настоящих данных, в большинстве случаев, хороши от обычных (см. главу 2.1). Отчего же распространено представление о двумерном обычном распределении? Дело в том, что теория в этом случае несложнее. В частности, равенство 0 теоретического коэффициента корреляции эквивалентно независимости случайных размеров.

Исходя из этого проверка независимости сводится к проверке статистической догадки о равенстве 0 теоретического коэффициента корреляции. Эта догадка принимается, в случае если

. где

— некое граничное значение, зависящее от количества выборки n и уровня значимости

.

В случае если предположение о двумерной нормальности не выполнено, то из равенства 0 теоретического коэффициента корреляции не вытекает независимость случайных размеров. Нетрудно выстроить пример случайного вектора, для которого коэффициент корреляции равен 0, но координаты зависимы. Помимо этого, для проверки догадок о коэффициенте корреляции нельзя пользоваться таблицами, вычисленными в предположении нормальности.

Возможно выстроить правила принятия ответов на базе асимптотической нормальности выборочного коэффициента корреляции. Но имеется и второй путь – перейти к непараметрическим коэффициентам корреляции, одинаково пригодным при любом постоянном распределении случайного вектора.

Для расчета непараметрического коэффициента ранговой корреляции Спирмена нужно сделать следующее. Для каждого xi вычислить его ранг ri в вариационном последовательности, выстроенном по выборке

Для каждого yi вычислить его ранг qi в вариационном последовательности, выстроенном по выборке

 Для комплекта из n пар

вычислить линейный коэффициент корреляции. Он именуется коэффициентом ранговой корреляции, потому, что определяется через ранги. Как пример разглядим эти из табл.1 (см. монографию [2]).

Таблица 1.

Эти для расчета коэффициентов корреляции

Источник: www.aup.ru

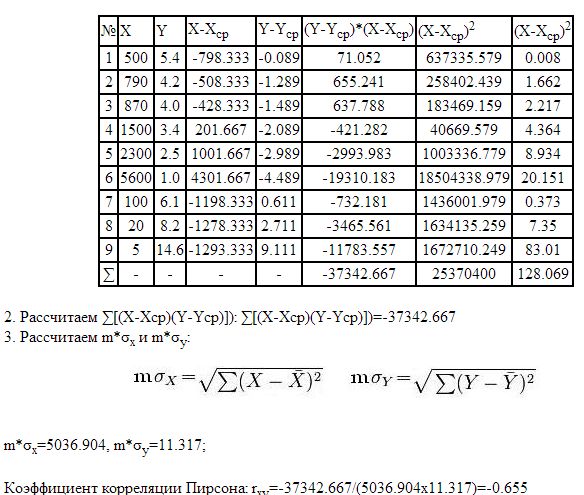
Коэффициент корреляции Пирсона. Пример

Самые интересные результаты статей, подобранные именно по Вашим интересам:

• Что такое точка безубыточности и как ее рассчитать

  В любом бизнесе принципиально важно вычислить, в какой момент предприятие всецело покроет убытки и начнет приносить настоящий доход. Для этого…

• Как рассчитать маржу форекс

  Справочник трейдера — Маржа Эта татья всецело посвящена такому понятию как Маржа. Вы определите как расчитывается маржа, от чего она зависит и как…

• Как рассчитать уровень инфляции

  Инфляция — факторы происхождения Инфляция — это переполнение каналов финансового обращения излишней финансовой массой. проявляемое в росте товарных…

• Как рассчитать индекс инфляции украина

  Индексация задолженности согласно соглашению: как вычислить Индексация заработной платы и других доходов наемных работников, и главных средств – понятия,…

• Какой доход от акций

  ЧАСТЬ 1: БАЗЫ РЫНКА ЦЕННЫХ БУМАГ Принцип оценки потенциальной денежной прибыли от акций совершенно верно такой же, как и для облигаций, т.е. доход от…

• Что будет если купить акции

  Недооцененные акции. Стоит ли брать? 26 Декабрь 2012 Недооцененные акции. Стоит ли брать? Если вы просматриваете данную статью, и наряду с этим являетесь…