Чему равно число фибоначчи

Posted by workscan on in Форекс и биржа

Чему равно число фибоначчи

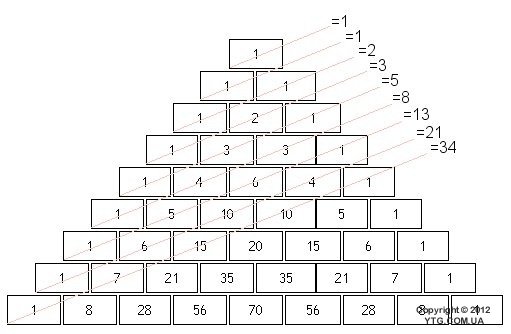
1.3. числа и Золотое сечение Фибоначчи

“Древние, — писал Г.Д.Гримм, — осознавали пропорцию следующим образом: “Две части либо две величины не смогут быть. связаны между собой без посредства третьей. Достигается это. п ропорцией (аналогией), в которой из трех чисел. среднее так относится ко второму, как первое к среднему, и второе к среднему, как среднее к первому” [50, с. 7]. Под пропорцией тут понимается отношение частей целого между собой и с целым; очевидна особенная роль среднего пропорционального.

Оно содержит в себе, как вычисляет М.А.Марутаев. “качественное обобщение, т.к. оно выражается одним числом, а не множеством” [89, с. 162]. Разумеется, что отдельные отношения и конкретные числа способны высказывать не только количество, но и “уровень качества”. Как раз исходя из этого пропорции так значительны в выражении гармонии.

Примером “качества”, представленного в отношении, есть золотое число. Итак, гармония связана с числами; это приводит к пропорциям особенного рода. Учение о золотом сечении появилось в следствии тщательного изучения природы чисел.

Считается, что деление отрезка в крайнем отношении и среднем в первый раз было осуществлено великим геометром и философом Старой Греции Пифагором, не смотря на то, что согласно точки зрения Б.Л.Ван-дер-Вардена [26] Пифагор, быть может, позаимствовал его у вавилонян и египтян. Было продемонстрировано, что отрезок единичной длины AB возможно поделить на две части точкой С так, что отношение большей части ( CB=x ) к меньшей (AС=1-x) будет равняться отношению всего отрезка (AB=1) к его большей части (CB): С B /AC=(AC+CB)/CB, т.е. x /(1-x) =1/ x. Из этого имеем алгебраическое выражение

x2 + x — 1 = 0.

Хорошим корнем этого уравнения есть (-1+ )/2, так что отношение 1/ х в разглядываемой пропорции равно

Такое деление Пифагор именовал золотым делением либо золотой пропорцией. Число 1,618 принято обозначать буквой Ф в честь древнегреческого скульптора Фидия, довольно часто применяющего золотую пропорцию в собственных творениях. В соответствии с делением в крайнем отношении и среднем единичный отрезок АВ точкой С делится следующим образом:

1. 0,618 = 0,618. 0,382 = 1,618

или иначе

0,382 + 0,618 = 1.

Письменные свидетельства, узнаваемые человечеству, о золотой пропорции в первый раз приводятся в ”Началах” Евклида (3 в. до н.э.). Евклид применял за пифагорейцами золотую пропорцию для построения верных десятиугольников и пятиугольников. Пятиугольник, правильнее пентаграмма, считался у пифагорейцев священным, потому, что эта фигура симметрична и одновременно с этим воплощает в себе некую асимметрию — золотую пропорцию, взятую соотношением неравных частей отрезка.

В силу собственных особенных особенностей пентаграмма считалась у пифагорейцев знаком здоровья и жизни. Существуют всего пять верных многогранников: четырехгранник (тетраэдр), шестигранник (куб), восьмигранник (октаэдр), двенадцатигранник (додекаэдр) и многогранник (икосаэдр). Все эти многогранники были известны древним грекам и стали называться платоновых тел по имени Платона, в первый раз их систематически обрисовавшим.

Каждое из них символизировало какое-то из 5 “начал” либо “стихий”: тетраэдр — тело огня, октаэдр — тело воздуха, гексаэдр (куб) — тело почвы, икосаэдр — тело воды, — додекаэдр — тело мира (мировом души, эфира либо разума). В средние века И.Кеплер (1571-1630) представил модель Нашей системы в форме последовательности положенных приятель в приятеля политонов ( платоновых тел).

Евклидом была продемонстрирована возможность построения всех верных многогранников на базе деления отрезка в крайнем отношении и среднем [73]. В последствии золотым делением занимались Гипоксил (2 в. до н.э.), Папп (3 в. до н.э.), Дж. Компано из Наварры (13 в .). Как вычисляет Э.М.Сороко [121], термин “золотое сечение” происходит от Птолемея.

Закрепилось это обозначение и стало популярным благодаря Леонардо да Винчи (1452-1519), что довольно часто его применял.

В 1202 г. вышло в свет произведение Liber abaci итальянского математика Леонардо Пизанского (1180-1240), известного, но, больше как Фибоначчи. В книге излагается множество задач. Одна из них ставится и решается следующим образом.

“какое количество пар кроликов в один год от одной пары рождается? Некто поместил несколько кроликов в некоем месте, огороженном со всех сторон стеной, дабы определить, сколько пар кроликов родится в течение года, в случае если природа кроликов такова, что через месяц пара кроликов создаёт на свет другую несколько, а рождают зайцы со второго месяца собственного рождения.

Так как 1-я пара в 1-м месяце дает потомство, удвой, и в этом месяце окажется две пары; из них одна пара, в частности первая, рождает и в следующем месяце, так что во втором месяце окажется 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родится еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5”, и т.д. Собственный ответ задачи Фибоначчи воображает так: “Мы складываем первое число со вторым, т.е.

1 и 2; и второе с третьим; и третье с четвертым; и без того одно за вторым, пока не сложим десятое с одиннадцатым, т.е. 144 и 233; и мы возьмём неспециализированное число кроликов, т.е. 377; и без того возможно делать по порядку до нескончаемого числа месяцев”. Обозначив число кроликов в n-ый месяц через fn. а в следующие месяцы — fn+1. fn+2 и т.д. последовательность чисел последовательности Фибоначчи возможно представить формулой

fn+2 = fn + fn+1.

И.Кеплер установил, что fn+1 / fn ® Ф. а Р.Симпсон (1687-1768) строго доказал, что

fn+1/ fn=Ф. В 1843 г. Ж.Бине отыскал формулу, определяющую n-член фибоначчиевой последовательности,

fn =( F -1/(-5) n ) /

.

Позднее было обнаружено, что не только хороший последовательность Фибоначчи, но и каждый последовательность с рекуррентным свойством с любыми начальными участниками a и b порождает последовательность a+b. a+2b, 2a+3b, 3a+5b, 5a+8b и т.д. отношение соседних участников которой по мере удаления от начала пытается к величине Ф =1,618. Примером таковой последовательности может служить последовательность Люка: 1, 3, 4, 7, 11, 18, 29, 47 и т.д.

С числами и золотым сечением Фибоначчи связаны целые области в культуре, практической деятельности и науке человека с древности до наших дней. Известно [121], что многие египетские архитектурные монументы выстроены на базе пропорции чисел и золотого сечения Фибоначчи. К примеру, с числами

55, 89, 144 связаны не только внешние пропорции пирамид, но и внутренние — зал фараона (пирамиды Хеопса, Хефрена и Микерина ). Золотая либо божественная пропорция, являясь чисто математическим соотношением, взяла широкое использование в архитектуре и творениях скульпторов Старой Греции. У древних греков все какое количество-нибудь большие архитектурные сооружения (храмы, стадионы, амфитеатры) выстроены так, что в них многообразно представлена золотая пропорция.

Фригийские гробницы и древний Парфенон, театр в Эпидавре и театр Диониса в Афинах — зодчества и яркие образцы ваяния, выполненные глубокой гармонии на базе золотого сечения. В случае если в Старом Египте закон золотого деления употребляется спорадически, то в Греции — неизменно. В средние века интерес к золотому сечению пропал и свойства данной пропорции были фактически забыты.

Влечение к “божественному сечению” быстро возросло в эру Ренессанса. Узнаваемый ученый, монах-минорит францисканского ордена Л. Пачоли ди Борго посвятил данной пропорции восторженную книгу “Божественная пропорция” (1509 г.). В данной книге [245] систематически излагались 12 разных особенностей гармонической пропорции. Характеризуя эти свойства, Пачолли пользовался очень сильными эпитетами: “необыкновенное”, “отличное”, “превосходное”, “практически сверхъестественное” и т.д.

Раскрывая данную пропорцию в качестве универсального отношения и в природе, и в мастерстве как совершенство красоты, он именовал ее “божественной” и склонен был ее разглядывать как “орудие мышления”, “эстетический закон”, как “природы и принцип мира”. Эта книга сопровождалась красивыми иллюстрациями Л. да Винчи, что “закрепил” за золотой пропорцией обозначение “золотое сечение” ( sectio aurea ). За Л. Пачолли И.Кеплер не меньше восторженно говорит о золотом сечении, именуя его божественным сечением ( sectio divina ). Он писал: “Геометрия обладает двумя сокровищами: одно из них — это теорема Пифагора, а второе — деление отрезка в крайнем отношении и среднем.

Первое возможно сравнить с мерой золота, второе же больше напоминает драгоценный камень” [217, c. 23]. Имеются свидетельства, что И.Кеплер одним из первых обратил внимание на проявления золотого сечения в ботанике. Особенно громадный интерес к золотой пропорции показали ученые, художники и зодчие 15-16 столетий, его обширно использовали в геометрии, мастерстве и особенно в архитектуре. В произведениях Браманте. Л. да Винчи, Рафаэля, Джорджане.

Тициана, Микельанджело и других проявляется строгая гармоничность и размерность сюжета, подчиняющаяся золотому сечению. Известные итальянские мастера Страдивариус, др и Амати. использовали золотое сечение и геометрию пентаграммы в очертаниях собственных скрипок. Шедеврами древнерусской архитектуры являются церковь Покрова на Нерли (12 в.), собор Василия Блаженного (16 в.), церковь Вознесения села Коломенское под Москвой (16 в.) и др.; в формах этих сооружений использованы элементы золотого сечения [27].

По окончании эры Ренессанса интерес к золотому сечению на большое время прервался и в течение более 200 лет эта пропорция была предана забвению. Только во второй половине 19 — начале 20 в.в. показались публикации, в которых золотое сечение в первый раз было установлено во многих закономерностях и явлениях биологических объектов. Среди них видное место занимают труды А.Цейзинга [296, 297]. Цейзинг разглядывал золотое сечение как фундаментальный морфологический закон в искусстве и природе.

Он продемонстрировал, что данный закон проявляется в пропорциях тела человека и в телах прекрасных животных. Г.Т.Фехнером [200] была установлена связь между психофизическим золотыми формами и “восприятием” человека предметов. Т.Кук [41] уделяет громадное внимание изучению роли логарифмической спирали в растительных и животных объектах.

Им установлено, что феномен роста в биологических объектах связан со спиралями золотого сечения. О значении золотой пропорции в искусстве и природе пишут Г.Тимеринг [125], Г.Д.Грим [50] и М.Гика [41], каковые приводят бессчётные примеры проявлений золотого сечения в явлениях природы и разных прикладных искусствах.

Занимательные изучения об применении золотой пропорции в шедеврах музыки, живописи и поэзии были совершены в в Российской Федерации и СССР Э.К.Розеновым [109], Л.Сабанеевым [112], Г.В.Церетели [154], М.А.Марутаевым [89], Н.А.Васютинским [27]. Выдающийся коммунистический режиссер С.М.Эйзенштейн [168] занимался изучением золотого сечения в кино. Он сознательно применял золотое сечение при структурном построении фильма “Броненосец Потемкин”, и при формировании отдельных кульминационных кадров фильма.

Много изучений посвящено проявлению золотого сечения в шедеврах древних мастеров и в современной архитектуре [110, 161 и др.]. А.Б.Рыбаков [110] уверен в том, что во многих архитектурных шедеврах древности золотое сечение проявляется по антропологическим показателям, т.к. золотая пропорция четко прослеживается в членении тела человека. Весьма интересно подчернуть, что установлена сообщение древних мер длины (локоть, ступня, разные сажени и т.д.) с золотым сечением.

Выдающийся французский архитектор Ле Корбюзье положил золотое сечение в базу собственной теории гармонизации в строительных работах, известную называющиеся совокупность “ Модулор ” [82]. В данной совокупности Ле Корбюзье объединил существующие представления о пропорциях людской тела с отношением золотой пропорции.

По окончании некоего ослабления внимания к золотому сечению в середине нынешнего столетия во второй его половине быстро возрос интерес к данной пропорции со стороны многих ученых в разных отраслях знаний. В Соединенных Штатах начал систематично выходить издание “ The Fibonacci Quarterly ”. В СССР публикуется последовательность работ, относящихся к разнообразным областям науки: поиску экстремумов унимодальных функций [128], математическом описании правил оптимизации живых совокупностей [22], организации Нашей системы [25], теории развития этнических культур [23], лечению некоторых болезней человека [54, 118, 124], в экономике [28].

Н.Н.Воробьев [38] продемонстрировал сообщение золотого сечения с теорией возвратных последовательностей, комбинаторной математикой, теорией чисел, геометрией, теорией поисков. Настоящий “взрыв” изучений по проблеме золотого сечения у нас приходится на последние 10-15 лет. В эти годы в СССР и бывших советских республиках показались большие работы в разных отраслях знаний, где золотая пропорц ее закономерности и ия использованы как необычный методологический принцип, лежащий в базе анализа технических и природных совокупностей, их структурной гармонии.

А.П.Стахов [122] развивает направление по приложению обобщенных золотых сечений и p-чисел Фибоначчи к ответу задач математической теории измерений и применению нетрадиционных способов в теории кодирования информации. Геометрическая интерпретация рекуррентного соотношения для р-чисел Фибоначчи возможно взята, в случае если мы поделим отрезок АВ точкой С в таком отношении, дабы AB/ CB=x. а CB/ ACp = xp. Значение искомого отношения АВ/ СВ сводится к ответу алгебраического уравнения

xp+1+ xp — 1 = 0.

Ниже приведены приближенные значения золотых р-пропорций. соответствующие начальным значениям р.

Источник: 314159.ru

Числа Фибоначчи

Важное на сайте:

Самые интересные результаты статей, подобранные именно по Вашим интересам: